首页 题库 比赛 评测 排名 讨论 帮助 返回比赛
登录 注册

F. 白金夜话

内存限制：256 MiB 时间限制：2000 ms 标准输入输出
题目类型：传统 评测方式：Special Judge
转到题库 提交记录 返回比赛

题目描述

いつまでも止まらない　この胸のときめきで　一緒に踊ろう
随着永不停息的这心中的悸动，一起来跳舞吧！

给定坐标平面上 n 个圆。任意两个圆的边界至多只有一个公共点 —— 即它们必定相离或相切。

对于一个圆的集合，定义其异或面积为平面上被该集合中奇数个圆覆盖的图形面积。

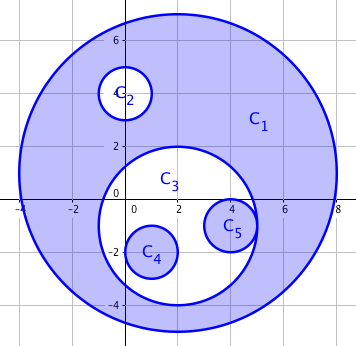
Figure 1

对于这个集合，浅蓝色部分图形的面积被计入异或面积内。

现在需要将这 $n$ 个圆划分为两个集合，每个圆恰好在两个集合中的一个内。

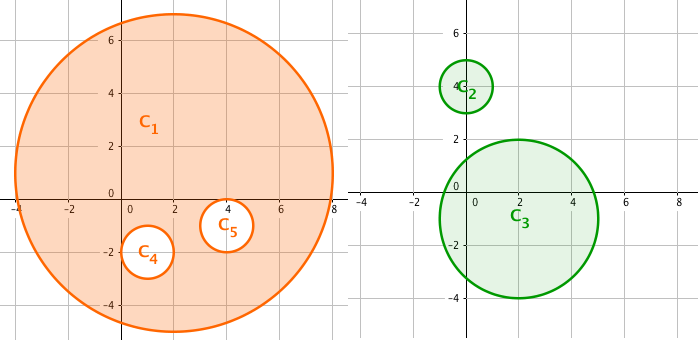
Figure 2

一种划分的方案，两个集合的异或面积如图所示。

请求出合法的划分方案中，两个集合分别计算的**异或面积**之和的最大值。

输入格式

输入的第一行包含一个正整数 n —— 圆的数目。

接下来 n 行，每行包含三个整数 x_i, y_i, r_i —— 描述一个圆心位于 (x_i, y_i) 、半径为 r_i 的圆。

输出格式

输出一个十进制实数 —— 合法的划分方案中，两个集合异或面积之和的最大值。

当选手答案与参考答案的相对误差或绝对误差不超过 10^{-9} 时被视为正确。形式化地，若选手输出为 a ，参考答案为 b ，答案被视为正确当且仅当 \frac{|a-b|}{\max{(1, |b|)}} \le 10^{-9} 。

样例

样例输入 1

5
2 1 6
0 4 1
2 -1 3
1 -2 1
4 -1 1

样例输出 1

138.23007676

样例解释 1

样例 1 的最优方案与「题目描述」一节中的图形对应。

样例输入 2

8
0 0 1
0 0 2
0 0 3
0 0 4
0 0 5
0 0 6
0 0 7
0 0 8

样例输出 2

289.02652413

数据范围与提示

1 \leq n \leq 1\,000
-10^6 \leq x_i, y_i \leq 10^6 ， 1 \leq r_i \leq 10^6

ささやかだけど　かけがえのない　歴史を重ねて
渺小平凡却无可替代的事物一点点重现着历史
偽りさえも　本当になる　君の隣りで
即使谎言在你身旁也会变得如此真实
　　　　　　　　　　　　　　　　　　——「白金ディスコ」

* 熬夜有害身体健康

LibreOJ Powered by SYZOJ.